Answer:
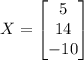
Explanation:
Our approach here is to isolate X, and simplify this solution. We want to begin by subtracting matrix 2, as shown below, from either side - the first step in isolating X. Afterwards we can multiply either side by the inverse of matrix 1, the co - efficient of X, such that X is now isolated. We can then simplify this value.
Given,
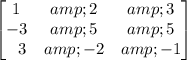 : Matrix 1
: Matrix 1
 : Matrix 2
: Matrix 2
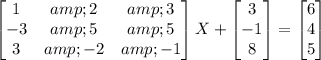 ( Subtract Matrix 2 from either side )
( Subtract Matrix 2 from either side )
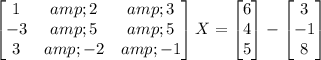 ( Simplify )
( Simplify )
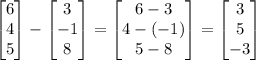 ( Substitute )
( Substitute )
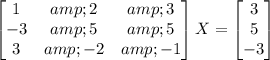 ( Multiply either side by inverse of Matrix 1 )
( Multiply either side by inverse of Matrix 1 )
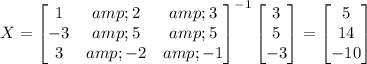 - let's say that this is Matrix 3. Our solution would hence be Matrix 3.
- let's say that this is Matrix 3. Our solution would hence be Matrix 3.