Question

For the functions f(x) = 4x^4+4x^3-8x^2-13x-5 and g(x) = x+1, find (f/g)(x) and (f/g)(2)

Answer 1

(f/g)(x) = 4x³ - 8x - 5

(f/g)(2) = 11

Explanation:

f(x) = 4x⁴ + 4x³ - 8x² - 13x - 5

g(x) = x + 1

To find (f/g)(2) first find (f/g)(x)

To find (f/g)(x) factorize f(x) first

That's

f(x) = 4x⁴ + 4x³ - 8x² - 13x - 5

f(x) = ( x + 1)( 4x³ - 8x - 5)

So we have

`(f/g)(x) = (( x + 1)( 4x³ - 8x - 5))/(x + 1)`

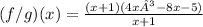
Simplify

We have

(f/g)(x) = 4x³ - 8x - 5

To find (f/g)(2) substitute 2 into (f/g)(x)

That's

(f/g)(2) = 4(2)³ - 8(2) - 5

= 4(8) - 16 - 5

= 32 - 16 - 5

= 11

(f/g)(2) = 11

Hope this helps you