Answer:
(a) and (a)
Explanation:
In both questions the denominator of the rational functions cannot be zero as this would make them undefined. Equating the denominators to zero and solving gives the values that x cannot be.
Given
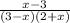
solve (3 - x)(2 + x) = 0
Equate each factor to zero and solve for x
3 - x = 0 ⇒ x = 3
2 + x = 0 ⇒ x = - 2
x = 3 and x = - 2 are excluded values → (a)
------------------------------------------------------------------------
Given
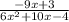
solve
6x² + 10x - 4 = 0 ← in standard form
(x+ 2)(6x - 2) = 0 ← in factored form
Equate each factor to zero and solve for x
x + 2 = 0 ⇒ x = - 2
6x - 2 = 0 ⇒ 6x = 2 ⇒ x =

x =
 and x = - 2 are excluded values → (a)
and x = - 2 are excluded values → (a)