Answer:
i
 a
a
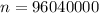
i
 b
b
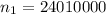
i
 c
c
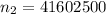
ii
 a
a
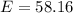
ii
 b
b
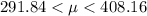 \
\
ii
 c
c
There is insufficient evidence to conclude that the analyst is right because the population mean fee by the analyst does not fall within the confidence interval
Explanation:
From the question we are told that
The sample size is
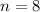
The sample mean is
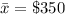
The sample standard deviation is
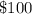
Considering question i
i
 a
a
At

given that the confidence level is 95% = 0.95
the level of significance would be
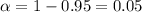
The critical value of
 from the normal distribution table is
from the normal distribution table is
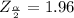
So the sample size is mathematically evaluated as
![n = [ \frac{Z_{(\alpha )/(2) } * \sigma }{E} ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/vwv2odauclk6lmr9vfh7htl4qx2fjlkg6i.png)
=>
![n =[ ( 1.96 * 100)/( 0.02) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/qp5t5gy6df9u58wfh7cqomwe8xfcfhzngs.png)
=>
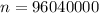
i
 b
b
At
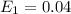 and confidence level = 95% =>
and confidence level = 95% =>
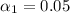 =>
=>
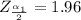
![n_1 = [ \frac{Z_{(\alpha_2 )/(2) } * \sigma }{E_1} ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/qrbdtia1q6kyshe8ex73tm3pjha4hw1eet.png)
=>
![n_1 =[ ( 1.96 * 100)/( 0.04) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/ipkxdgcvxhosf6vkst8kz4y62kfehbijv7.png)
=>
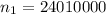
i
 c
c
At
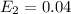 confidence level = 99% =>
confidence level = 99% =>

The critical value of
 from the normal distribution table is
from the normal distribution table is
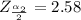
=>
![n_2 = [ \frac{Z_{(\alpha_2 )/(2) } * \sigma }{E_2} ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/fhlrjak8vt79m2yryerrnx337k73et08t1.png)
=>
![n_2 =[ ( 2.58 * 100)/( 0.04) ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/pe54oh89imnlbhgt3yz64ccsf24ys1i43w.png)
=>
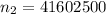
Considering ii
Given that the level of significance is
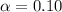
Then the critical value of
 from the normal distribution table is
from the normal distribution table is
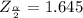
Generally the margin of error is mathematically represented as
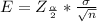
substituting values
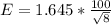
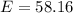
Generally the 90% confidence interval is mathematically evaluated as
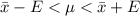
=>
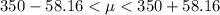
=>
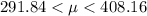
So the interpretation is that there is 90% confidence that the mean fee charged to H&R Block customers last year is in the interval .So there is insufficient evidence to conclude that the analyst is right because the population mean fee by the analyst does not fall within the confidence interval.