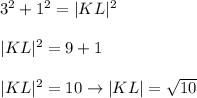Answer:
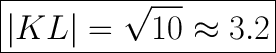
Explanation:
METHOD 1:
The formula of a distance between two points (x₁; y₁) and (x₂; y₂):
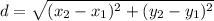
We have K(-1; -3) and L(0; 0). Substitute:
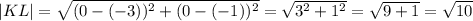
METHOD 2:
Look at the picture.
We have the right triangle with the legs 3 and 1.
Use the Pythagorean theorem:
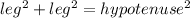
substitute: