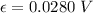Question

A 6.7 cm diameter circular loop of wire is in a 1.27 T magnetic field. The loop is removed from the field in 0.16 ss . Assume that the loop is perpendicular to the magnetic field.

Required:
What is the average induced emf?

Answer 1

The induced emf is
`\epsilon = 0.0280 \ V`

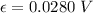
Step-by-step explanation:

From the question we are told

The diameter of the loop is
`d = 6.7 cm = 0.067 \ m`

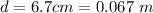
The magnetic field is
`B = 1.27 \ T`

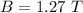
The time taken is
`dt = 0.16 \ s`

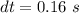
Generally the induced emf is mathematically represented as

`\epsilon = - N * (\Delta \phi)/(dt)`

Where N = 1 given that it is only a circular loop

`\Delta \phi = \Delta B * A`

Where
`\Delta B = B_f - B_i`

where
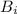`B_i` is 1.27 T given that the loop of wire was initially in the magnetic field

and
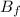`B_f` is 0 T given that the loop was removed from the magnetic field

Now the area of the of the loop is evaluated as

`A = \pi r^2`

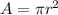
Where r is the radius which is mathematically represented as

`r = (d)/(2)`

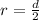
substituting values

`r = (0.067)/(2)`

`r = 0.0335 \ m`

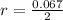
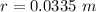
So

`A = 3.142 * (0.0335)^2`

`A = 0.00353 \ m^2`

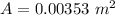
So

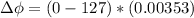
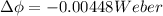
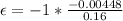
`\Delta \phi = (0- 127)* (0.00353)`

`\Delta \phi = -0.00448 Weber`

=>
`\epsilon = - 1 * (-0.00448)/(0.16)`

=>
`\epsilon = 0.0280 \ V`