Question

The hot glowing surfaces of stars emit energy in the form of electromagnetic radiation. It is a good approximation to assume that the emissivity eee is equal to 1 for these surfaces.

Required:
a. Find the radius RRigel of the star Rigel, the bright blue star in the constellation Orion that radiates energy at a rate of 2.7 x 10^31 W and has a surface temperature of 11,000 K.
b. Find the radius RProcyonB of the star Procyon B, which radiates energy at a rate of 2.1 x 10^23 W and has a surface temperature of 10,000 K. Assume both stars are spherical. Use σ=5.67 x 10−8^ W/m^2*K^4 for the Stefan-Boltzmann constant.

Answer 1

Given that,

Energy
`H=2.7*10^(31)\ W`

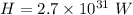
Surface temperature = 11000 K

Emissivity e =1

(a). We need to calculate the radius of the star

Using formula of energy

`H=Ae\sigma T^4`

`A=(H)/(e\sigma T^4)`

`4\pi R^2=(H)/(e\sigma T^4)`

`R^2=(H)/(e\sigma T^4*4\pi)`

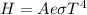
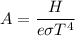
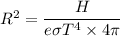
Put the value into the formula

`R=\sqrt{(2.7*10^(31))/(1*5.67*10^(-8)*(11000)^4* 4\pi)}`

`R=5.0*10^(10)\ m`

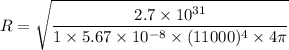
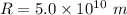
(b). Given that,

Radiates energy
`H=2.1*10^(23)\ W`

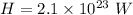
Temperature T = 10000 K

We need to calculate the radius of the star

Using formula of radius

`R^2=(H)/(e\sigma T^4*4\pi)`

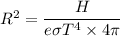
Put the value into the formula

`R=\sqrt{(2.1*10^(23))/(1*5.67*10^(-8)*(10000)^4*4\pi)}`

`R=5.42*10^(6)\ m`

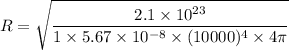
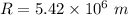
Hence, (a). The radius of the star is
`5.0*10^(10)\ m`

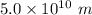
(b). The radius of the star is
`5.42*10^(6)\ m`