Question

What is the measure of the acute angle formed by the lines 3x–5y=–15 and 4x+2y=7?

Answer 1

85.6 degrees.

Explanation:

The given equations of lines are

`3x-5y=-15`

`4x+2y=7`

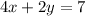
We need to find the measure of the acute angle formed by these lines.

`Slope=\frac{-\text{Coefficient of }x}{\text{Coefficient of }y}`

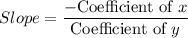
Slope of given lines are

`m_1=(-3)/(-5)=(3)/(5)`

`m_2=(-4)/(2)=-2`

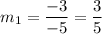
Angle between two lines is

`\tan \theta = \left|(m_1-m_2)/(1+m_1m_2)\right|`

`\tan \theta = \left|((3)/(5)-(-2))/(1+(3)/(5)(-2))\right|`

`\tan \theta = \left|((3+10)/(5))/((5-6)/(5))\right|`

`\tan \theta = \left|(13)/(1)\right|`

`\tan \theta = 13`

`\theta = \tan^(-1)(13)`

`\theta \approx 85.6^(\circ)<90^(\circ)`

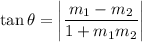
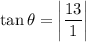
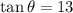
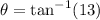
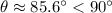
Therefore, the acute angle between given lines is 85.6 degrees.