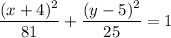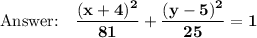
Explanation:
A "horizontal" ellipse means that the x-radius is bigger than the y-radius. Thus, x is the major axis and y is the minor axis.
The equation of an ellipse is:
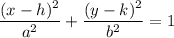 where
where
- (h, k) is the center of the ellipse
- a is the radius on the x-axis
- b is the radius on the y-axis
It is given that the center is at (-4, 5) --> h = -4, k = 5
It is given that the major axis has a length of 18 --> x-radius = 9
It is given that the minor axis has a length of 10 --> y-radius = 5
Input those values into the equation of an ellipse to get:
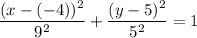
Simplify to get: