Question

What the answer now

Answer 1

35.6 yd²

Explanation:

Area of ∆UVW can be solved if we know the lengths of 2 sides and their included angle.

We are Given just 1 side, UV (w). Use the law of sines to find UW (v).

Thus:

`(v)/(sin(V)) = (w)/(sin(W))`

W = 137°

w = 19 yd

V = 180 - (137 + 22) = 21° => sum of triangle

v = ??

Plug in the values and solve for v

`(v)/(sin(21)) = (19)/(sin(137))`

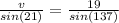
Multiply both sides by sin(21)

`(v)/(sin(21))*sin(21) = (19)/(sin(137))*sin(21)`

`v = (19*sin(21))/(sin(137))`

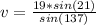
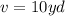`v = 10 yd` (approximated)

Find area of ∆UVW:

Area = ½*UV*UW*sin(U)

Area = ½*v*w*sin(U)

= ½*10*19*sin(22)

Area = 35.6 yd² (to nearest tenth)