Question

Is the function ƒ(θ) = 2cos( θ) an odd or even function?

Answer 1

It’s an Even function

Answer 2

Even function.

Explanation:

An odd function has symmetry with respect to the origin.

`\text{A function is odd }\Leftrightarrow f(-x)=-f(x)`

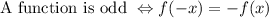
The sine function is an odd function:

`\sin(-\theta)=\sin(\theta)`

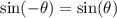
An even function has symmetry with respect to the y-axis.

`\text{A function is even}\Leftrightarrow f(-x)=f(x)`

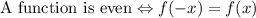
The cosine function is an even function:

`\cos(-\theta)=\cos(\theta)`

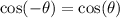
Is the function
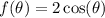`f(\theta)=2\cos(\theta)` an odd or even function?

It is an even function.

What happens in the function is a vertical stretch by a factor of 2. The y-intercept is equal to 2.