Question

To the nearest whole percent, what is the probability that a randomly chosen member of the JV swim team does not wear glasses and is in the 10th grade? 14% 17% 55% 67%

Answer 1

Answer: 14%

Explanation:

Complete question is provided in the attachment below:

Probability that members of the junior varsity swim team wear glasses = 55%=0.55

Given: P(wear glasses) = 0.55

P(not wear glasses) = 1-0.55 = 0.45

P(member in 10th grade | not wear glasses) = 30%

Using conditional probability formula:

`P(B|A)=\frac{P(A\text{ and } B)}{P(A)}`

`\Rightarrow\ 0.30=\frac{P(\text{not wear glasses and in 10th grade})}{0.45}\\\\\Rightarrow\ P(\text{not wear glasses and in 10th grade})=0.45*0.30\\\\0.135=13.5\%\approx14\%`

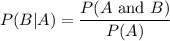
Hence, the probability that a randomly chosen member of the JV swim team does not wear glasses and is in the 10th grade = 14%.

So, the correct option is "14%".