Question

6. Find the focus for the parabola.
2x=(y+3)^2+14
Focus: (x,y) =

Answer 1

Answer: Focus = (7.5, -3)

Explanation:

The Vertex form of a horizontal parabola is: x = a(y - k)² + h where

• a is the vertical stretch;
  `a=(1)/(4p)`
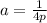
• p is the distance from the vertex to the focus
• (h, k) is the vertex

Rewrite the equation in Vertex form to identify a, h, & k:

2x = (y + 3)² + 14

`x=((y+3)^2+14)/(2)\\\\x=(1)/(2)(y+4)^2+7`

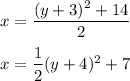
Vertex: (h, k) = (7, -3)

`a=(1)/(2)`

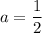
Find p and then find the focus: Focus = (h + p, k)

`a=(1)/(4p)\quad \rightarrow \quad (1)/(2)=(1)/(4p)\quad \rightarrow \quad 4p=2\quad \rightarrow \quad p=(2)/(4)\quad \rightarrow p=(1)/(2)\\`

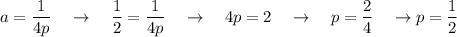
Focus: (7 +
`(1)/(2)` , -3) = (7.5, -3)