Question

Michael records the height of 1000 people. This data is a normal distribution and the sample mean was 0.75. Identify the margin of error for this data set.

Answer 1

0.0284

Explanation:

The formula for calculating the Margin of error of a dataset is expressed as;

Margin of error =
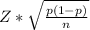`Z*\sqrt{(p(1-p))/(n) } \\\\` where;

Z is the z-score of 95% confidence interval = 1.96

p is the sample proportion/mean = 0.75

n is the sample size = total number of people = 1000

Note that when the confidence interval is not given, it is always safe to use 95% confidence.

Substituting this values into the formula we have;

`ME = 1.96*\sqrt{(0.7(1-0.7))/(1000) } \\\\ME = 1.96*\sqrt{(0.7(0.3))/(1000) } \\\\ME = 1.96*√(0.00021) } \\\\ME = 1.96*0.01449\\\\ME = 0.0284`

Hence the margin error for the dataset is 0.0284