Answer:
-16128
Explanation:
This expression can be calculated by algebraic means, whose process is described below:
1)
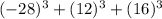 Given.
Given.
2)
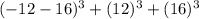 Definition of addition.
Definition of addition.
3)
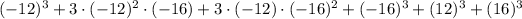 Cubic perfect binomial.
Cubic perfect binomial.
4)
![(12)^(3)+[(-1)\cdot (12)]^(3)+(16)^(3) + [(-1)\cdot (16)]^(3)+3 \cdot (-12)^(2)\cdot (-16) + 3\cdot (-12)\cdot (-16)^(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/svsvjyy4xzjcyx5tf7kgvz6dcpvtgr57qe.png) Commutative property/
Commutative property/
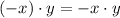
5)
![(12)^(3) + (-1)^(3)\cdot (12)^(3) + 16^(3) +(-1)^(3)\cdot (16)^(3) + (-3)\cdot [(-12)^(2)\cdot (16) +(-16)^(2)\cdot (12)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/svn9k02bhvzqktl3j8118fzq34bd9ah564.png) Distributive property/
Distributive property/
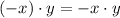 /
/
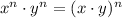
6)
![(12)^(3) + [-(12)^(3)]+(16)^(3) + [-(16)^(3)]+ (-3)\cdot [(-12)^(2)\cdot (16)+(-16)^(2)\cdot (12)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ldfjm1mjzv0r0bgtrij7afse1xf5q7h2tp.png)
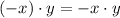
7)
![(-3)\cdot [(-12)^(2)\cdot (16) + (-16)^(2)\cdot (12)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/2m7ez18qx7gg4v6u1y6n0jzfx7lrbd74gy.png) Existence of the additive inverse/Modulative property for addition.
Existence of the additive inverse/Modulative property for addition.
8)
![(-3) \cdot [(12)^(2)\cdot (16)+(16^(2))\cdot (12)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9gwqsmrweukyjc22emb2w1hoyuhtzbid54.png)
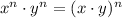 /
/
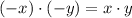
9)
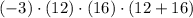 Distributive property.
Distributive property.
10)
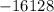
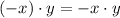 /Definition of sum/Definition of multiplication/Result
/Definition of sum/Definition of multiplication/Result