Answer:
Explanation:
Given two series A and B;
Series A: 10 + 4 +8/5 + 16/25 + 13/125 + ...
Series B: 1/5 + 3/5 + 9/5 + 27/5 + 81/5 +...
Both series are geometric series since they have the same common ratio. Given the geometric series T₁, T₂, T₃, T₄..., the common ratio r is expressed as
 .
.
a) For series A, Given T₁ = 10, T₂ = 4, T₃ = 8/5 and T₄ = 13/125
Its common ratio is expressed as
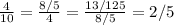
Hence the common ratio of series A is 2/5
The sum to infinity of the geometric series will be expressed as

Note that the sum to infifnity is used since the series is tending to infinity.
a is the first term if the series = 10
r - 2/5
On substituting this values into the formula;
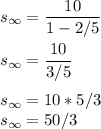
Hence the sum of the series is 50/3
b) For the series B;
Series B: 1/5 + 3/5 + 9/5 + 27/5 + 81/5 +...
The common ratio of the series is expressed as shown;
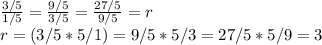
Hence its common ratio is 3.
Sun of the series is expressed similarly as:
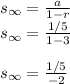
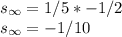
Hence the sum of series B is -1/10