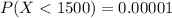Answer:
a
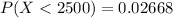
b
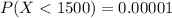
Explanation:
From the question we are told that
The population mean is
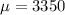
The standard deviation is

We also told in the question that the birth weight is approximately Normally distributed
i.e
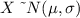
Given that Low-birth-weight babies weighing less than 2500 grams,then the proportion of babies born full term are low-birth-weight babies is mathematically represented as
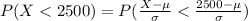
Generally
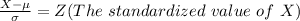
So

substituting values
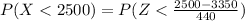
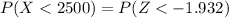
Now from the standardized normal distribution table(These value can also be obtained from Calculator dot com) the value of
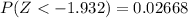
=>
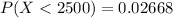
Given that very-low-birth-weight babies (weighing less than 1500 grams,then the proportion of babies born full term are very-low-birth-weight babies is mathematically represented as

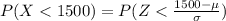
substituting values
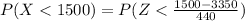
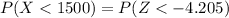
Now from the standardized normal distribution table(These value can also be obtained from calculator dot com) the value of