Question

F(x)=3x2+10x-25 g(x)=9x2-25 Find (f/g)(x).

Answer 1

`(f/g)(x) = (x + 5)/(3x + 5)`

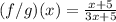
Explanation:

f(x) = 3x² + 10x - 25

g(x) = 9x² - 25

To find (f/g)(x) divide f(x) by g(x)

That's

`(f/g)(x) = \frac{3 {x}^(2) + 10x - 25 }{9 {x}^(2) - 25 }`

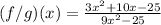
Factorize both the numerator and the denominator

For the numerator

3x² + 10x - 25

3x² + 15x - 5x - 25

3x ( x + 5) - 5( x + 5)

(3x - 5 ) ( x + 5)

For the denominator

9x² - 25

(3x)² - 5²

Using the formula

a² - b² = ( a + b)(a - b)

(3x)² - 5² = (3x + 5)(3x - 5)

So we have

`(f/g)(x) = ((3x - 5)(x + 5))/((3x + 5)(3x - 5))`

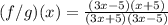
Simplify

We have the final answer as

`(f/g)(x) = (x + 5)/(3x + 5)`

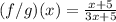
Hope this helps you