Question

When sketching a normal curve, what

value represents one standard deviation

to the right of the mean for the data set?

56, 54, 45, 52, and 48.

Answer 1

The value representing one standard deviation to the right of the mean is 55.

Explanation:

The provided data set is:

S = {56, 54, 45, 52, and 48}

Compute the mean and standard deviation as follows:

`\mu=(1)/(n)\sum X=(1)/(5)* [56+54+45+52+48]=51\\\\\sigma=\sqrt{(1)/(n)\sum (X-\mu)^(2)}=\sqrt{(1)/(5)\cdot {(56-51)^(2)+...+(48-51)^(2)}}=\sqrt{(1)/(5)* 80}=4`

Compute the value representing one standard deviation to the right of the mean as follows:

`X=\mu+1\cdot \sigma`

`=51+(1* 4)\\=51+4\\=55`

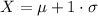
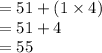
Thus, the value representing one standard deviation to the right of the mean is 55.