Question

In RST, RS = 7, RT = 10, and ST = 8. Which angle of RST has the smallest measure? A T BCANNT BE DETERMINDED C R D S

Answer 1

Correct answer is option A. T

Explanation:

Given that

In a
`\triangle RST`, RS = 7, RT = 10, and ST = 8.

To find:

Smallest angle = ?

Solution:

We can use cosine rule here to find the angle.

Formula for cosine rule:

`cos B = (a^(2)+c^(2)-b^(2))/(2ac)`

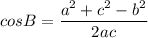
Where

a is the side opposite to
`\angle A`

b is the side opposite to
`\angle B`

c is the side opposite to
`\angle C`

Using the cosine rule:

`cos T = (ST^(2)+RT^(2)-RS^(2))/(2* ST * RT)\\\Rightarrow cos T = (8^(2)+10^(2)-7^(2))/(2* 8 * 10)\\\Rightarrow cos T = (64+100-49)/(160)\\\Rightarrow cos T = (115)/(160)\\\Rightarrow \angle T = cos^(-1)(0.71875)\\\Rightarrow \angle T = 44.05^\circ`

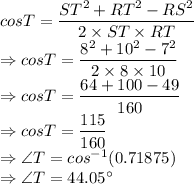
Now, let us use Sine rule to find other angles:

`(a)/(sinA) = (b)/(sinB) = (c)/(sinC)`

`(RS)/(sinT) = (ST)/(sinR) = (RT)/(sinS)\\\Rightarrow (7)/(sin44.05) = (8)/(sinR) = (10)/(sinS)\\\Rightarrow (7)/(0.695) = (8)/(sinR) = (10)/(sinS)\\\Rightarrow sin R = (8 * 0.695)/(7)\\\Rightarrow R = 52.58^\circ`

`\Rightarrow sin S = (10 * 0.695)/(7)\\\Rightarrow S = 83.14^\circ`

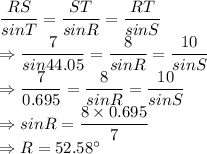
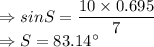
Smallest angle is
`\angle T`

Correct answer is option A. T