Question

An Uber driver provides service in city A and city B only dropping off passengers and immediately picking up a new one at the same spot. He finds the following Markov dependence. For each trip, if the driver is in city A, the probability that he has to drive passengers to city B is 0.25. If he is in city B, the probability that he has to drive passengers to city A is 0.45. Required:a. What is the 1-step transition matrix? b. Suppose he is in city B, what is the probability he will be in city A after two trips? c. After many trips between the two cities, what is the probability he will be in city B?

Answer 1

a. 1-step transition matrix is be expressed as:

`P= \left[\begin{array}{cc}0.75&0.25\\0.45&0.55\\\end{array}\right]`

b. The probability that he will be in City A after two trips given that he is in City B = 0.585

c. After many trips, the probability that he will be in city B = 0.3571

Explanation:

Given that:

For each trip, if the driver is in city A, the probability that he has to drive passengers to city B is 0.25

If he is in city B, the probability that he has to drive passengers to city A is 0.45.

The objectives are to calculate the following :

a. What is the 1-step transition matrix?

To determine the 1 -step transition matrix

Let the State ∝ and State β denotes the Uber Driver providing service in City A and City B respectively.

∴ The transition probability from state ∝ to state β is 0.25.

The transition probability from state ∝ to state ∝ is 1- 0.25 = 0.75

The transition probability from state β to state ∝ is 0.45. The transition probability from state β to state β is 1 - 0.45 = 0.55

Hence; 1-step transition matrix is be expressed as:

`P= \left[\begin{array}{cc}0.75&0.25\\0.45&0.55\\\end{array}\right]`

b. Suppose he is in city B, what is the probability he will be in city A after two trips?

Consider
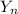`Y_n` = ∝ or β to represent the Uber driver is in City A or City B respectively.

∴ The probability that he will be in City A after two trips given that he is in City B

=
`P(Y_0 = 2, Y_2 = 1 , Y_3 = 1) + P(Y_0 = 2, Y_2 = 2 , Y_3 = 1)`

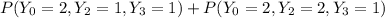
= 0.45 × 0.75 + 0.55 × 0.45

= 0.3375 + 0.2475

= 0.585

c. After many trips between the two cities, what is the probability he will be in city B?

Assuming that Ф = [ p q ] to represent the long run proportion of time that Uber driver is in City A or City B respectively.

Then, ФP = Ф , also p+q = 1 , q = 1 - p and p = 1 - q

∴

`[ p\ \ \ q ] = \left[\begin{array}{cc}0.75&0.25\\0.45&0.55\\\end{array}\right] [ p\ \ \ q ]`

0.75p + 0.45q = q

-0.25p + 0.45q = 0

since p = 1- q

-0.25(1 - q) + 0.45q = 0

-0.25 + 0.25 q + 0.45q = 0

0.7q = 0.25

q =
`\frac{0.25} {0.7 }`

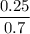
q = 0.3571

After many trips, the probability that he will be in city B = 0.3571