Answer:
The answer to this question can be defined as follows:
In option A: The answer is "13020".
In option B: The answer is "468 Segments".
Step-by-step explanation:
Given:
The value of round-trip delay= 60 m-second
The value of Bandwidth= 1Gbps
The value of Segment size = 576 octets
window size =?
Formula:
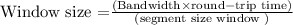
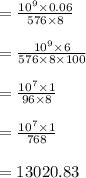
So, the value of the segments is =13020.833 or equal to 13020
Calculating segments in the size of 16 k-bytes:
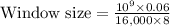
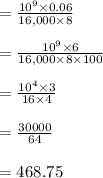
The size of 16 k-bytes segments is 468.75 which is equal to 468.