Question

Researchers recorded that a certain bacteria population declined from 120,000 to 200 in 36 hours. At this rate of decay, how many bacteria will there be in 31 hours? Round to the nearest whole number.

Answer 1

Answer: There will 486 bacteria in 31 hours.

Explanation:

The population decay in bacteria is exponential.

Exponential function :
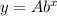`y=Ab^x`, where A = initial population, b multiplication decay factor, t= time:

As per given:

Initial population:
`A=120,000`

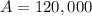
After 36 hours, population =
`120000(b^(36))=200`

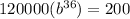
Divide both sides by 120,000 we get

`b^(36)= 0.00167`

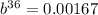
Taking natural log on both sides , we get

`36\ln b=\ln 0.00167\\\\\Rightarrow\ b=e^{\left((\ln0.00167)/(36)\right)}=0.83724629\approx0.8372`

At x= 31,

`y=120000(0.8372)^(31)=120000*0.00405234\approx486`

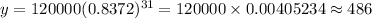
Hence, there will 486 bacteria in 31 hours.