Answer:
Approximately
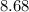 .
.
Step-by-step explanation:
The
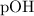 of a solution can be found from the hydroxide ion concentration
of a solution can be found from the hydroxide ion concentration
![\rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/loneh06ylg80japtk5kbej6yd1zmn5yg1o.png) with the following equation:
with the following equation:
![\displaystyle \rm pOH = -\log_(10) \rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/bhib7u3qe9zw87d9qtk9auwncp2i4r8bgk.png) .
.
On the other hand, the ion-product constant of water,
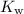 , relates the hydroxide ion concentration
, relates the hydroxide ion concentration
![\rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/loneh06ylg80japtk5kbej6yd1zmn5yg1o.png) of a solution to its hydronium ion concentration
of a solution to its hydronium ion concentration
![\rm \left[{H_3O}^(+)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/vu87sli4kbrtfhxfkrq7zatpz8izcge9ug.png) :
:
![K_\text{w} = \rm \left[{H_3O}^(+)\right] \cdot \rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/ws2b85qk6uttxgskhuo4j928ypzhskxwli.png) .
.
- At
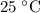 ,
,
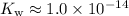 .
. - For this particular
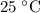 solution,
solution,
![\rm \left[{H_3O}^(+)\right] = 4.8 * 10^(-6)\; \rm mol \cdot L^(-1)](https://img.qammunity.org/2021/formulas/chemistry/college/2kfdr5pd8ha576bra6wax0oscauvhbbl9s.png) .
.
Hence the
![\rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/loneh06ylg80japtk5kbej6yd1zmn5yg1o.png) of this solution:
of this solution:
![\begin{aligned}\left[\mathrm{OH}^(-)\right] &= \frac{K_\text{w}}{\rm \left[{H_3O}^(+)\right]} \\ &= (1.0 * 10^(-14))/(4.8 * 10^(-6))\; \rm mol\cdot L^(-1) \approx 2.08333 * 10^(-9)\; \rm mol\cdot L^(-1)\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/ymxvfdi48qg4kowxfhnzhp7c0sykbfpu2w.png) .
.
Therefore, the
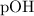 of this solution would be:
of this solution would be:
![\begin{aligned}\rm pOH &= -\log_(10) \rm \left[OH^(-)\right] \\ &\approx -\log_(10) \left(4.8 * 10^(-6)\right) \approx 8.68\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/3v4navx4cfwqp60n2ib97owi467wiwwiuf.png) .
.
Note that by convention, the number of decimal places in
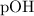 should be the same as the number of significant figures in
should be the same as the number of significant figures in
![\rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/loneh06ylg80japtk5kbej6yd1zmn5yg1o.png) .
.
For example, because the
![\rm \left[{H_3O}^(+)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/vu87sli4kbrtfhxfkrq7zatpz8izcge9ug.png) from the question has two significant figures, the
from the question has two significant figures, the
![\rm \left[OH^(-)\right]](https://img.qammunity.org/2021/formulas/chemistry/college/loneh06ylg80japtk5kbej6yd1zmn5yg1o.png) here also has two significant figures. As a result, the
here also has two significant figures. As a result, the
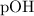 in the result should have two decimal places.
in the result should have two decimal places.