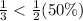Question

During April of 2013, Gallup randomly surveyed 500 adults in the US, and 47% said that they were happy, and without a lot of stress." Calculate and interpret a 95% confidence interval for the proportion of U.S. adults who considered themselves happy at that time. 1 How many successes and failures are there in the sample? Are the criteria for approximate normality satisfied for a confidence interval?

A What is the sample proportion?
B compute the margin of error for a 95% confidence interval.
C Interpret the margin of error you calculated in Question 1
C. Give the lower and upper limits of the 95% confidence interval for the population proportion (p), of U.S. adults who considered themselves happy in April, 2013.
D Give an interpretation of this interval.
E. Based on this interval, is it reasonably likely that a majority of U.S. adults were happy at that time?
H If someone claimed that only about 1/3 of U.S. adults were happy, would our result support this?

Answer 1

number of successes

`k = 235`

number of failure

`y = 265`

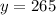
The criteria are met

A

The sample proportion is
`\r p = 0.47`

B

`E =4.4 \%`

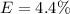
C

What this mean is that for N number of times the survey is carried out that the which sample proportion obtain will differ from the true population proportion will not more than 4.4%

Ci

`r = 0.514 = 51.4 \%`

`v = 0.426 = 42.6 \%`

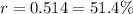
D

This 95% confidence interval mean that the the chance of the true population proportion of those that are happy to be exist within the upper and the lower limit is 95%

E

Given that 50% of the population proportion lie with the 95% confidence interval the it correct to say that it is reasonably likely that a majority of U.S. adults were happy at that time

F

Yes our result would support the claim because

`(1)/(3 ) \ of N < (1)/(2) (50\%) \ of \ N , \ Where\ N \ is \ the \ population\ size`

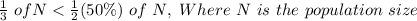
Explanation:

From the question we are told that

The sample size is
`n = 500`

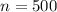
The sample proportion is
`\r p = 0.47`

Generally the number of successes is mathematical represented as

`k = n * \r p`

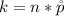
substituting values

`k = 500 * 0.47`

`k = 235`

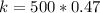
Generally the number of failure is mathematical represented as

`y = n * (1 -\r p )`

substituting values

`y = 500 * (1 - 0.47 )`

`y = 265`

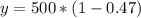
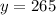
for approximate normality for a confidence interval criteria to be satisfied

`np > 5 \ and \ n(1- p ) \ >5`

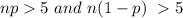
Given that the above is true for this survey then we can say that the criteria are met

Given that the confidence level is 95% then the level of confidence is mathematically evaluated as

`\alpha = 100 - 95`

`\alpha = 5 \%`

`\alpha =0.05`

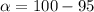
Next we obtain the critical value of
`(\alpha )/(2)` from the normal distribution table, the value is

`Z_{( \alpha )/(2) } = 1.96`

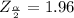
Generally the margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) } * \sqrt{ (\r p (1- \r p)/(n) }`

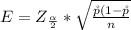
substituting values

`E = 1.96 * \sqrt{ (0.47 (1- 0.47)/(500) }`

`E = 0.044`

=>
`E =4.4 \%`

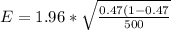
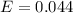
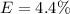
What this mean is that for N number of times the survey is carried out that the proportion obtain will differ from the true population proportion of those that are happy by more than 4.4%

The 95% confidence interval is mathematically represented as

`\r p - E < p < \r p + E`

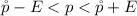
substituting values

`0.47 - 0.044 < p < 0.47 + 0.044`

`0.426 < p < 0.514`

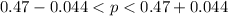
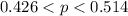
The upper limit of the 95% confidence interval is
`r = 0.514 = 51.4 \%`

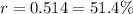
The lower limit of the 95% confidence interval is
`v = 0.426 = 42.6 \%`

This 95% confidence interval mean that the the chance of the true population proportion of those that are happy to be exist within the upper and the lower limit is 95%

Given that 50% of the population proportion lie with the 95% confidence interval the it correct to say that it is reasonably likely that a majority of U.S. adults were happy at that time

Yes our result would support the claim because

`(1)/(3 ) < (1)/(2) (50\%)`