Answer:
Explanation:
The summary of the given statistics data include:
sample size n = 400
sample mean
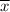 = 6.86
= 6.86
standard deviation = 4.37
Level of significance ∝ = 0.01
Population Mean
 = 6.00
= 6.00
Assume that a simple random sample has been selected. Identify the null and alternative hypotheses, test statistic, P-value, and state the final conclusion that addresses the original claim.
To start with the hypothesis;
The null and the alternative hypothesis can be computed as :
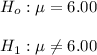
The test statistics for this two tailed test can be computed as:
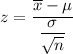
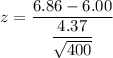
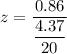
z = 3.936
degree of freedom = n - 1
degree of freedom = 400 - 1
degree of freedom = 399
At the level of significance ∝ = 0.01
P -value = 2 × (z < 3.936) since it is a two tailed test
P -value = 2 × ( 1 - P(z ≤ 3.936)
P -value = 2 × ( 1 -0.9999)
P -value = 2 × ( 0.0001)
P -value = 0.0002
Since the P-value is less than level of significance , we reject
 at level of significance 0.01
at level of significance 0.01
Conclusion: There is sufficient evidence to conclude that the original claim that the mean of the population of earthquake depths is 5.00 km.