Question

AB = 3.2 cm

BC= 8.4 cm
The area of triangle ABC is 10 cm²
Calculate the perimeter of triangle ABC.
Give your answer correct to three significant figures.​

Answer 1

Therefore, perimeter of the given triangle is 18.300 cm.

Explanation:

Area of the triangle ABC =
`(1)/(2)(\text{AB})(\text{BC})(\text{SinB})`

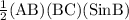
10 =
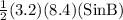
`(1)/(2)(3.2)(8.4)(\text{SinB})`

Sin(B) =
`(10)/(3.2* 4.2)`

B =
`\text{Sin}^(-1)(0.74405)`

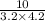
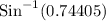
B = 48.08°

By applying Cosine rule in the given triangle,

(AC)² = (AB)² + (BC)²-2(AB)(BC)CosB

(AC)² = (3.2)² + (8.4)² - 2(3.2)(8.4)Cos(48.08)°

(AC)² = 10.24 + 70.56 - 35.9166

(AC)² = 44.88

AC =
`√(44.8833)`

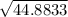
AC = 6.6995 cm

Perimeter of the ΔABC = m(AB) + m(BC) + m(AC)

= 3.200 + 8.400 + 6.6995

= 18.2995

≈ 18.300 cm

Therefore, perimeter of the given triangle is 18.300 cm