Question

The point (6, 6) is on the graph y = f(x) . Find the corresponding coordinates of this point on the graph y = 4f[1/3x +9] -7

a. (-9,17)
b. (17,-9)
c. (11,11)
d. (9,17)

Answer 1

Correct answer is:

a. (-9,17)

Explanation:

We are given that a point (6, 6) lies on the graph of
`y =f(x)`.

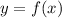Putting the values from the given point:

`6 =f(6)`

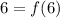
That means we are given that
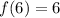`f(6) =6` ..... (1)

And we have to find the corresponding coordinates of this point on the graph of
`y = 4f[\frac{1}3x +9] -7`

From equation (1), we know the value of
`f(6)`.

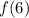so, let us convert
`f[\frac{1}3x +9]` to a form such that it becomes equal to
`f(6)`

`\Rightarrow (1)/(3)x +9 =6\\\Rightarrow (1)/(3)x=-3\\\Rightarrow x = -9`

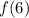
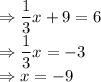
So, let us put
`x = -9` in the given function:

`4f[\frac{1}3* (-9) +9] -7\\\Rightarrow 4f[-3 +9] -7\\\Rightarrow 4f(6) -7`

Now, using equation (1), putting
`f(6)=6`

`\Rightarrow 4* 6 -7\\\Rightarrow 24-7 \\\Rightarrow y = 17`

Therefore, the point the corresponding point is:

a. (-9,17)