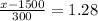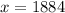Question

The SAT Reasoning Test (formerly called the Scholastic Aptitude Test) is perhaps the most widely used standardized test for college admissions in the United States. Scores are based on a normal distribution with a mean of 1500 and a standard deviation of 300. Clinton College would like to offer an honors scholarship to students who score in the top 10 percent of this test. What is the minimum score that qualifies for the scholarship?

Minimum Score:

Answer 1

The score is
`x = 1884`

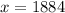
Explanation:

From the question we are told that

The population mean is
`\mu = 1500`

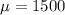
The standard deviation is
`\sigma = 300`

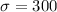
From the question we are told that the score follow a normal distribution

i.e
`X \~ \ N( 1500 , 300)`

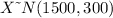
The proportion of score in the top 10% is mathematically

`P(X > x ) = P( (X - \mu)/(\sigma ) > (x - \mu)/(\sigma ) ) = 0.10`

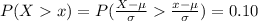
Where x is the minimum score required to be in the top 10%

Now the
`(X - \mu)/(\sigma ) = Z (The \ Standardized \ value \ of \ X)`

So

`P(X > x ) = P( Z > (x - \mu)/(\sigma ) ) = 0.10`

So

`P(X > x ) = P( Z > (x - 1500)/(300) ) = 0.10`

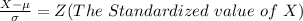
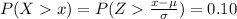
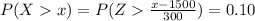
So the critical value of 0.10 from the normal distribution table is
`Z_(0.10) = 1.28`

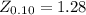
So

`(x - 1500)/(300) = 1.28`

`x = 1884`