Question

Astronomers discover an exoplanet (a planet of a star other than the Sun) that has an orbital period of 3.75

Earth years in its circular orbit around its sun, which is a star with a measured mass of 3.23×1030kg
. Find the radius of the exoplanet's orbit.

Answer 1

`r=4.24* 10^(11)\ m`

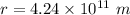
Step-by-step explanation:

Given that,

Orbital time period, T = 3.75 earth years

Mass of star,
`m=3.23* 10^(30)\ kg`

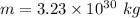
We need to find the radius of the exoplanet's orbit. It is a concept of Kepler's third law of motion i.e.

`T^2=(4\pi^2)/(GM)r^3`

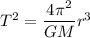
r is the radius of the exoplanet's orbit.

Solving for r we get :

`r=((T^2GM)/(4\pi^2))^(1/3)`

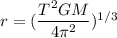
We know that,
`1\ \text{earth year}=3.154* 10^7\ \text{s}`

So,

`r=(((3.75* 3.154* 10^7)^2* 6.67* 10^(-11)* 3.23* 10^(30))/(4\pi^2))^(1/3)\\\\r=4.24* 10^(11)\ m`

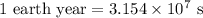
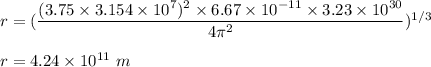
So, the radius of the exoplanet's orbit is
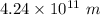`4.24* 10^(11)\ m`.