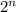Answer:
The additional words is
Step-by-step explanation:
Given
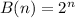
Required
Determine the additional words; i.e.
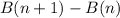
From the given parameters, we have that;
B is a function of n
Such that;
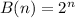
To calculate
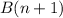 , we simply substitute n + 1 for n
, we simply substitute n + 1 for n
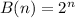
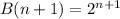
Applying laws of indices
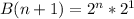
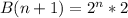
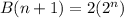
Calculating Additional Binary Code;
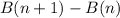
Substitute values for B(n + 1) and B(n)
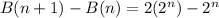
Express
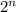 as
as
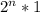
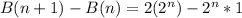
Express 1 as
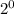
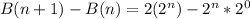
Factorize
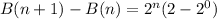
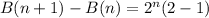
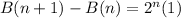
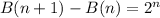
Hence, the additional words is