Question

A pool ball moving 1.83 m/s strikes an identical ball at rest. Afterward, the first ball moves 1.15 m/s at a 23.3 degrees angle. What is the y-component of the velocity of the second ball?

Answer 1

v_{1fy} = - 0.4549 m / s

Step-by-step explanation:

This is an exercise of conservation of the momentum, for this we must define a system formed by the two balls, so that the forces during the collision have internal and the momentum is conserved

initial. Before the crash

p₀ = m v₁₀

final. After the crash

`p_(f)` = m
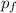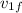`v_(1f)` + m v_{2f}

Recall that velocities are a vector so it has x and y components

p₀ = p_{f}

we write this equation for each axis

X axis

m v₁₀ = m v_{1fx} + m v_{2fx}

Y Axis

0 = -m v_{1fy} + m v_{2fy}

the exercise tells us the initial velocity v₁₀ = 1.83 m / s, the final velocity v_{2f} = 1.15, let's use trigonometry to find its components

sin 23.3 = v_{2fy} / v_{2f}

cos 23.3 = v_{2fx} / v_{2f}

v_{2fy} = v_{2f} sin 23.3

v_{2fx} = v_{2f} cos 23.3

we substitute in the momentum conservation equation

m v₁₀ = m v_{1f} cos θ + m v_{2f} cos 23.3

0 = - m v_{1f} sin θ + m v_{2f} sin 23.3

1.83 = v_{1f} cos θ + 1.15 cos 23.3

0 = - v_{1f} sin θ + 1.15 sin 23.3

1.83 = v_{1f} cos θ + 1.0562

0 = - v_{1f} sin θ + 0.4549

v_{1f} sin θ = 0.4549

v_{1f} cos θ = -0.7738

we divide these two equations

tan θ = - 0.5878

θ = tan-1 (-0.5878)

θ = -30.45º

we substitute in one of the two and find the final velocity of the incident ball

v_{1f} cos (-30.45) = - 0.7738

v_{1f} = -0.7738 / cos 30.45

v_{1f} = -0.8976 m / s

the component and this speed is

v_{1fy} = v1f sin θ

v_{1fy} = 0.8976 sin (30.45)

v_{1fy} = - 0.4549 m / s