Question

Listed below are numbers of internet users per 100 people and numbers of scientific award winners per 10 million people for different countries. construct aâ scatterplot, find the value of the linear correlation coefficientâ r, and find theâ p-value of r. determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. use a significance level of alpha α equals = 0.05 0.05. internet users 78.0 78.0 79.0 79.0 56.2 56.2 68.3 68.3 77.9 77.9 38.2 38.2 award winners 5.5 5.5 8.8 8.8 3.3 3.3 1.7 1.7 10.8 10.8 0.1 0.1

Answer 1

There is not sufficient evidence to support a claim of linear correlation between the two variables.

Explanation:

The data provided is as follows:

X Y

78 5.5

79 8.8

56.2 3.3

68.3 1.7

77.9 10.8

38.2 0.1

(a)

The scatter plot is attached below.

(b)

Use the Excel function: =CORREL(array1, array2) to compute the correlation coefficient, r.

The correlation coefficient between the number of internet users and the award winners is,

r = 0.797.

(c)

The test statistic value is:

`t=r\sqrt{(n-2)/(1-r^(2))}`

`=0.797*\sqrt{(6-2)/(1-(0.797)^(2))}\\\\=0.797* 3.311372\\\\=2.639163484\\\\\approx 2.64`

The degrees of freedom is,

df = n - 2

= 6 - 2

= 4

Compute the p-value as follows:

`p-value=P(t_(n-2)<2.64)=0.057`

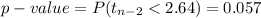
*Use a t-table.

p-value = 0.057 > α = 0.05

The null hypothesis will not be rejected.

Thus, it can be concluded that there is not sufficient evidence to support a claim of linear correlation between the two variables.