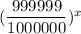Answer:
The probability mass function that you never win
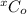 =
=
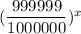
Explanation:
Given that;
the winning chance of a weekly local lottery =

=
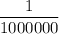
The probability of losing = 1 - probability of winning (winning chance)
The probability of losing =
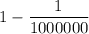
The probability of losing =
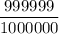
The probability mass function that you never win
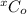 =
=
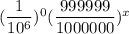
The probability mass function that you never win
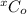 =
=