Answer:
(a) The probability that X is at most 30 is 0.9726.
(b) The probability that X is less than 30 is 0.9554.
(c) The probability that X is between 15 and 25 (inclusive) is 0.7406.
Explanation:
We are given that 11% of all steel shafts produced by a certain process are nonconforming but can be reworked. A random sample of 200 shafts is taken.
Let X = the number among these that are nonconforming and can be reworked
The above situation can be represented through binomial distribution such that X ~ Binom(n = 200, p = 0.11).
Here the probability of success is 11% that this much % of all steel shafts produced by a certain process are nonconforming but can be reworked.
Now, here to calculate the probability we will use normal approximation because the sample size if very large(i.e. greater than 30).
So, the new mean of X,
 =
=
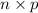 =
=
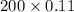 = 22
= 22
and the new standard deviation of X,
 =
=
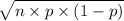
=
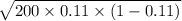
= 4.42
So, X ~ Normal(
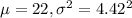 )
)
(a) The probability that X is at most 30 is given by = P(X < 30.5) {using continuity correction}
P(X < 30.5) = P(
 <
<
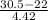 ) = P(Z < 1.92) = 0.9726
) = P(Z < 1.92) = 0.9726
The above probability is calculated by looking at the value of x = 1.92 in the z table which has an area of 0.9726.
(b) The probability that X is less than 30 is given by = P(X
 29.5) {using continuity correction}
29.5) {using continuity correction}
P(X
 29.5) = P(
29.5) = P(


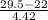 ) = P(Z
) = P(Z
 1.70) = 0.9554
1.70) = 0.9554
The above probability is calculated by looking at the value of x = 1.70 in the z table which has an area of 0.9554.
(c) The probability that X is between 15 and 25 (inclusive) is given by = P(15
 X
X
 25) = P(X < 25.5) - P(X
25) = P(X < 25.5) - P(X
 14.5) {using continuity correction}
14.5) {using continuity correction}
P(X < 25.5) = P(
 <
<
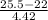 ) = P(Z < 0.79) = 0.7852
) = P(Z < 0.79) = 0.7852
P(X
 14.5) = P(
14.5) = P(


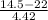 ) = P(Z
) = P(Z
 -1.70) = 1 - P(Z < 1.70)
-1.70) = 1 - P(Z < 1.70)
= 1 - 0.9554 = 0.0446
The above probability is calculated by looking at the value of x = 0.79 and x = 1.70 in the z table which has an area of 0.7852 and 0.9554.
Therefore, P(15
 X
X
 25) = 0.7852 - 0.0446 = 0.7406.
25) = 0.7852 - 0.0446 = 0.7406.