Question

A line passes through the points (3,0) and (4,2). What is its equation in slope-intercept form?

Answer 1

y = 2x - 6

Explanation:

Slope intercept form:

Equation of the line:

`\sf \boxed{ y = mx +b}`

Here m is the slope and b is the y-intercept.

Step 1: Find the slope

(3 , 0) ⇒ x₁ = 3 & y₁ = 0

(4 , 2) ⇒ x₂ = 4 & y₂ = 2

`\sf \boxed{Slope=(y_2-y_1)/(x_2-x_1)}`

`\sf = (2 -0)/(4-3)\\\\= (2)/(1)\\\\=2`

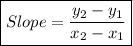
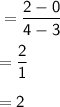
m = 2

Step2: Now, substitute the value of 'm' in the equation.

y = 2x + b

Step3: In the above equation plug in any point. Here, (3 ,0) is chosed.

0 = 2*3 + b

0 = 6 + b

-6 = b

b = -6

Step4: Equation of the line:

y = 2x - 6