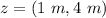Answer:
a
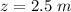
b
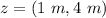
Step-by-step explanation:
From the question we are told that
Their distance apart is
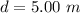
The wavelength of each source wave
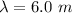
Let the distance from source A where the construct interference occurred be z
Generally the path difference for constructive interference is
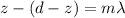
Now given that we are considering just the straight line (i.e points along the line connecting the two sources ) then the order of the maxima m = 0
so

=>

=>
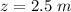
Generally the path difference for destructive interference is
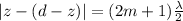
=>
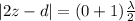
=>
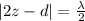
substituting values
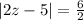
=>
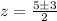
So
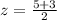
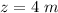
and
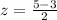
=>
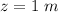
=>