Question

Let $S$ be the set of complex numbers of the form $a + bi,$ where $a$ and $b$ are integers. We say that $z \in S$ is a unit if there exists a $w \in S$ such that $zw = 1.$ Find the number of units in $S.$

Answer 1

Number of units possible in S are 4.

Step-by-step explanation:

Given S is a set of complex number of the form
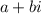`a+bi` where a and b are integers.

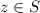`z\in S` is a unit if
`w\in z` exists such that
`zw=1`.

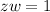To find:

Number of units possible = ?

Solution:

Given that:

`zw = 1`

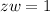
Taking modulus both sides:

`|zw| = |1|`

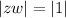
Using the property that modulus of product of two complex numbers is equal to their individual modulus multiplied.

i.e.

`|z_1z_2|=|z_1|.|z_2|`

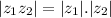
So,

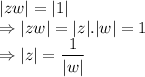`|zw| = |1|\\\Rightarrow |zw| =|z|.|w| =1\\\Rightarrow |z|=(1)/(|w|)`......... (1)

Let
`z=a+bi`

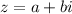
Then modulus of z is
`|z| = √(a^2+b^2)`

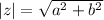
Given that a and b are integers, so the equation (1) can be true only when
`|z| = |w| =1` (Reciprocal of 1 is 1). Modulus can be equal only when one of the following is satisfied:

(a = 1, b = 0) , (a = -1, b = 0), (a = 0, b = 1) OR (a = 0, b = -1)

So, the possible complex numbers can be:

`1.\ 1 + 0i = 1\\2.\ -1 + 0i = -1\\3.\ 0+ 1i = i\\4.\ 0 -1i = -i`

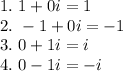
Hence, number of units possible in S are 4.