Question

Does the table represent a linear function ??

Answer 1

No, because the points on the table need to have a constant slope for the function to be linear.

Answer 2

No.

Explanation:

The points from the table need to have a constant slope for the function to be linear.

Slope is rise over run.

`m=(y_2-y_1)/(x_2-x_1)`

For (1,1) and (2,2):

`m=(2-1)/(2-1)=(1)/(1)=\boxed{1}`

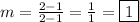
The slope is 1.

For (3,6) and (4,24):

`m=(24-6)/(4-3)=(18)/(1)=\boxed{18}`

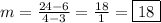
The slope is 18.

1 ≠ 18

Since the slopes of the points are no consistent, the table represents a nonlinear function.

Therefore,

The table does NOT represent a linear function.