Question

Last school year, in the school of Business Administration, 30% were Accounting majors, 24% Management majors, 26% Marketing majors, and 20% Economics majors. A sample of 300 students taken from this year's students of the school showed the following number of students in each major: Accounting 83 Management 68 Marketing 85 Economics 64 Total 300 Has there been any significant change in the number of students in each major between the last school year and this school year?

Answer 1

The proportions of Accounting and Economics majors remained relatively consistent, while the proportions of Management and Marketing majors decreased slightly between last school year and this school year.

Step-by-step explanation:

To determine if there has been a significant change in the number of students in each major between last school year and this school year, we can compare the proportions of students in each major from the two samples. In the last school year, the proportions were: Accounting - 30%, Management - 24%, Marketing - 26%, Economics - 20%. In the current school year sample, the proportions are: Accounting - 27.67%, Management - 22.67%, Marketing - 28.33%, Economics - 20.67%. By comparing these proportions, we can see that the proportions of Accounting and Economics majors stayed relatively consistent, while the proportions of Management and Marketing majors decreased slightly.

Answer 2

There has been no significant change in the number of students in each major between the last school year and this school year.

Step-by-step explanation:

A Chi-square test for goodness of fit will be used in this case.

The hypothesis can be defined as:

H₀: There has been no change in the number of students.

Hₐ: There has been a significant change in the number of students.

The test statistic is given as follows:

`\chi^(2)=\sum\limits^(n)_(i=1)((O_(i)-E_(i))^(2))/(E_(i))`

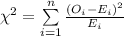
Here,

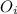`O_(i)` = Observed frequencies

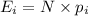`E_(i)=N* p_(i)` = Expected frequency.

The chi-square test statistic value is, 1.662.

The degrees of freedom is:

df = 4 - 1 = 4 - 1 = 3

Compute the p-value as follows:

`p-value=P(\chi^(2)_(k-1) >1.662) =P(\chi^(2)_(3) >1.662) =0.645`

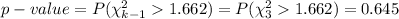
*Use a Chi-square table.

The p-value is 0.645.

The p-value of the test is very large for all the commonly used significance level. The null hypothesis will not be rejected.

Thus, it can be concluded that the there has been no significant change in the number of students in each major between the last school year and this school year.