Question

Company a samples 16 workers, and their average time with the company is 5.2 years with a standard deviation of 1.1. Company b samples 21 workers and their average time with the company is 4.6 years with a standard deviation 4.6 years

Answer 1

Company a samples 16 workers, and their average time with the company is 5.2 years with a standard deviation of 1.1. Company b samples 21 workers and their average time with the company is 4.6 years with a standard deviation 4.6 years

The populations are normally distributed. Determine the:

Hypothesis in symbolic form?

Determine the value of the test statistic?

Find the critical value or value?

determine if you should reject null hypothesis or fail to reject?

write a conclusion addressing the original claim?

Answer:

Explanation:

GIven that :

Company A

Sample size n₁ = 16 workers

Mean
`\mu`₁ = 5.2

Standard deviation
`\sigma`₁ = 1.1

Company B

Sample size n₂ = 21 workers

Mean
`\mu`₂ = 4.6

Standard deviation
`\mu`₂ = 4.6

The null hypothesis and the alternative hypothesis can be computed as follows:

`H_o : \mu _1 = \mu_2`

`H_1 : \mu _1 > \mu_2`

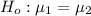
The value of the test statistics can be determined by using the formula:

`t = \frac{\overline {x_1}- \overline {x_2}}{\sqrt{\sigma p^2( (1)/(n_1)+(1)/(n_2))}}`

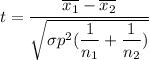
where;

`\sigma p^2= ((n_1 -1) \sigma_1^2+ (n_2-1)\sigma_2^2)/(n_1+n_2-2)`

`\sigma p^2= ((16 -1) (1.1)^2+ (21-1)4.6^2)/(16+21-2)`

`\sigma p^2= ((15) (1.21)+ (20)21.16)/(35)`

`\sigma p^2= (18.15+ 423.2)/(35)`

`\sigma p^2= (441.35)/(35)`

`\sigma p^2= 12.61`

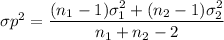
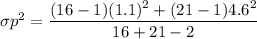
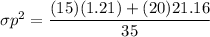
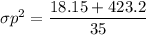
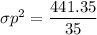
Recall:

`t = \frac{\overline {x_1}- \overline {x_2}}{\sqrt{\sigma p^2( (1)/(n_1)+(1)/(n_2))}}`

`t = \frac{5.2- 4.6}{\sqrt{12.61( (1)/(16)+(1)/(21))}}`

`t = \frac{0.6}{\sqrt{12.61( (37)/(336))}}`

`t = (0.6)/(√(12.61(0.110119)))`

`t = (0.6)/(√(1.38860059))`

`t = (0.6)/(1.178388981)`

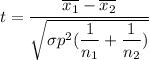
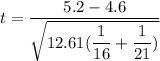
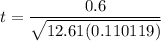
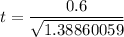
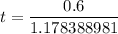
t = 0.50917

degree of freedom df = ( n₁ + n₂ - 2 )

degree of freedom df = (16 + 21 - 2)

degree of freedom df = 35

Using Level of significance ∝ = 0.05, From t-calculator , given that t = 0.50917 and degree of freedom df = 35

p - value = 0.3069

The critical value
`t_(\alpha ,d.f)` =
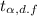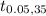`t_(0.05 , 35)` = 1.6895

Decision Rule: Reject the null hypothesis if the test statistics is greater than the critical value.

Conclusion: We do not reject the null hypothesis because, the test statistics is lesser than the critical value, therefore we conclude that there is no sufficient information that the claim that company a retains it workers longer than more than company b.