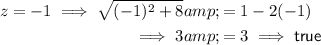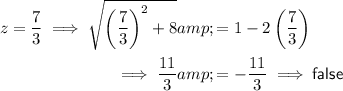Question

Avery solves the equation below by first squaring both sides of the equation.

Answer 1

z = 7/3 is extraneous.

Explanation:

√(z^2+8) = 1 - 2z

z^2 + 8 = (1 - 2z)^2

z^2 + 8 = 1 -4z + 4z^2

3z^2 - 4z - 7 = 0

3z^2 + 3z - 7z - 7 = 0

3z(z + 1) - 7(z + 1) = 0

(3z - 7)(z + 1) = 0

3z = 7, z = -1

z = 7/3, -1.

One of these might be extraneous.

Checking:

√(z^2+8) = 1 - 2z, if z = -1:

√(1 + 8) = 3, -3

1 - 2(-1) = 3. So its not z = -1

if z = 7/3

√((7/3)^2 + 8) = 13.44

1 - 2(7/3) = -3.66

So its z = 7/3

Answer 2

`z=(7)/(3)`

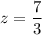
Explanation:

Given equation:

`√(z^2+8)=1-2z`

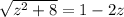
Square both sides:

`\implies (√(z^2+8))^2=(1-2z)^2`

`\implies z^2+8=1-4z+4z^2`

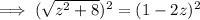
Subtract
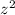`z^2` from both sides:

`\implies 8=1-4z+3z^2`

Subtract 8 from both sides:

`\implies 0=-7-4z+3z^2`

`\implies 3z^2-4z-7=0`

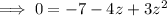
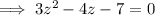
Rewrite the middle term:

`\implies 3z^2+3z-7z-7=0`

Factor the first two terms and the last two terms separately:

`\implies 3z(z+1)-7(z+1)=0`

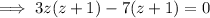
Factor out the common term
`(z+1)`:

`\implies (3z-7)(z+1)=0`

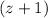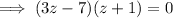
Therefore:

`\implies (z+1)=0 \implies z=-1`

`\implies (3z-7)=0 \implies z=(7)/(3)`

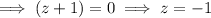
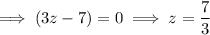
To find the extraneous solution (the root that is not a root of the original equation), enter the two found values of z into the original equation:

`\begin{aligned}z=-1\implies √((-1)^2+8)&=1-2(-1)\\\implies 3&=3\implies \textsf{true}\\\end{aligned}`

`\begin{aligned}z=(7)/(3) \implies \sqrt{\left((7)/(3)\right)^2+8}&=1-2\left((7)/(3)\right)\\\implies (11)/(3) &=-(11)/(3)\implies \textsf{false}\end{aligned}`

`\textsf{As}\: (11)/(3) \\eq -(11)/(3)\:\textsf{then}\: z=(7)/(3)\:\textsf{is the extraneous solution}`