Question

The average life of individual is 70 years. With a standard deviation of 5.5 years. Assume that the lives of these individuals is normally distributed. a. Find the probability that a mean life of a random sample of 5 such turtles falls between 60 and 80 years. b. Find the mean data value that separates the top 10% from the rest of the means computed from a random sample of size 5.

Answer 1

The answer is below

Explanation:

Given that:

mean (μ) = 70 years, standard deviation (σ)= 5.5 years.

a) The z score measures how many standard deviation a raw score is above or below the mean. It is given as:

`z=(x-\mu)/(\sigma)`, for a sample size of n, the z score is:
`z=(x-\mu)/(\sigma/√(n) )`

Given a sample of 5 turtles, we have to calculate the z score for x = 60 and x = 80.

For x = 60:

`z=(x-\mu)/(\sigma/√(n) )=(60-70)/(5.5/√(5) ) =-4.07`

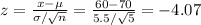
For x = 80:

`z=(x-\mu)/(\sigma/√(n) )=(80-70)/(5.5/√(5) ) =4.07`

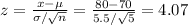
The probability that a mean life of a random sample of 5 such turtles falls between 60 and 80 years = P(60 < x < 80) = P(-4.07 < z < 4.07) = P(z < 4.07) - P(z < -4.07) = 1 - 0 = 1 = 100%

b) The z score that corresponds to top 10% is -1.28.

`z=(x-\mu)/(\sigma/√(n) )\\\\-1.28=(x-70)/(5.5/√(5) )\\ x-70=-3\\x=70-3\\x=67\ years`