Answer:
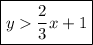
Option B is the correct option.
Explanation:
point ₁ ( - 3 , - 1 ) x₁ = - 3 , y₂ = - 1
point ₂ ( 3 , 3 ). x₂ = 3 , y₂= 3
Now, let's find the slope:
Slope ( m ) =
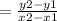
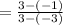
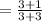
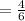
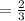
At ( 3 , - 1 )
y = mx + c , where m is the gradient / slope amd c is called the intercept on y-axis
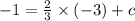
Solve for c
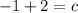
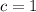
Since, The red line is dotted line. Therefore it does not include the equal to part. And the shaded region is upper part. Hence, ' > ' should be used.
The answer would be:
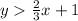
Hope I helped!
Best regards!