Answer:
The 95% confidence interval for the difference in population means is (−26.325175 , 36.325175)
Explanation:
Given that :
sample size n₁ = 36
sample mean
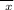 ₁ = 83
₁ = 83
standard deviation
 ₁ = 5
₁ = 5
sample size n₂ = 49
sample mean
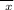 ₂= 78
₂= 78
standard deviation
 ₂ = 3
₂ = 3
The objective is to construct a 95% confidence interval for the difference in the population means
Let the population means be
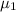 and
and
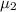
The 95% confidence interval or the difference in population means can be calculated by using the formula;
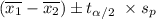
where;
the pooled standard deviation
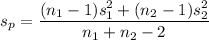
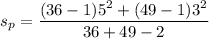
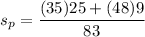
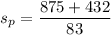
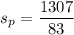
 = 15.75
= 15.75
degree of freedom =
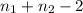
degree of freedom = 36+49 -2
degree of freedom = 85 - 2
degree of freedom = 83
The Critical t- value 95% CI at df = 83 is
t critical = T.INV.2T(0.05, 83) = 1.9889
Therefore, for the population mean , we have:
= (83 - 78) ± (1.9889 × 15.75)
= 5 ± 31.325175
= 5 - 31.325175 , 5 + 31.325175
= (−26.325175 , 36.325175)