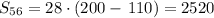Question

The common difference of an ap is -2 find its sum of first term is hundred and last term is minus 10

Answer 1

The sum of the arithmetic progression is 2520

Explanation:

The sum, Sₙ, of an arithmetic progression, AP, is given as follows;

`S_(n)=(n)/(2)\cdot \left (2\cdot a+\left (n-1 \right )\cdot d \right )`

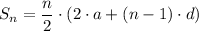
Where;

n = The nth term of the progression

a = The first term = 100

d = The common difference = -2

Given that the last term = -10, we have;

-10 = 100 + (n - 1) ×(-2)

n = (-10 - 100)/(-2) + 1 = 56

Therefore, the sum of the 56 terms of the arithmetic progression is
`S_(56)=(56)/(2)\cdot \left (2\cdot 100+\left (56-1 \right )\cdot (-2) \right )`

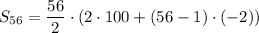
Which gives;

`S_(56)={28}\cdot \left (200-\left 110 \right ) = 2520`