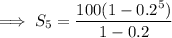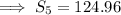Question

Find the sum of the geometric series 100+20+…+0.16

Answer 1

c) 124.96

Explanation:

Geometric series: 100 + 20 + ... + 0.16

First we need to find which term 0.16 is.

General form of a geometric sequence:
`a_n=ar^(n-1)`

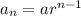
(where a is the first term and r is the common ratio)

To find the common ratio r, divide one term by the previous term:

`\implies r=(a_2)/(a_1)=(20)/(100)=0.2`

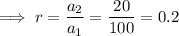
Therefore,
`a_n=100(0.2)^(n-1)`

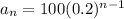
Substitute
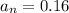`a_n=0.16` into the equation and solve for n:

`\implies 100(0.2)^(n-1)=0.16`

`\implies (0.2)^(n-1)=0.0016`

`\implies \ln(0.2)^(n-1)=\ln0.0016`

`\implies (n-1)\ln(0.2)=\ln0.0016`

`\implies n-1=(\ln0.0016)/(\ln(0.2))`

`\implies n=(\ln0.0016)/(\ln(0.2))+1`

`\implies n=5`

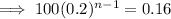
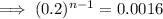
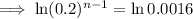
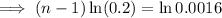
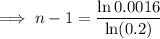
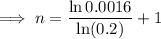
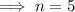
Therefore, we need to find the sum of the first 5 terms.

Sum of the first n terms of a geometric series:

`S_n=(a(1-r^n))/(1-r)`

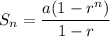
Therefore, sum of the first 5 terms:

`\implies S_5=(100(1-0.2^5))/(1-0.2)`

`\implies S_5=124.96`