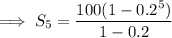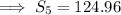Answer:
c) 124.96
Explanation:
Geometric series: 100 + 20 + ... + 0.16
First we need to find which term 0.16 is.
General form of a geometric sequence:
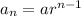
(where a is the first term and r is the common ratio)
To find the common ratio r, divide one term by the previous term:
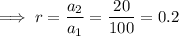
Therefore,
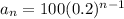
Substitute
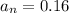 into the equation and solve for n:
into the equation and solve for n:
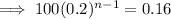
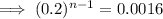
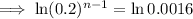
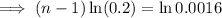
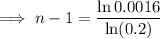
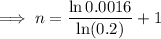
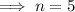
Therefore, we need to find the sum of the first 5 terms.
Sum of the first n terms of a geometric series:
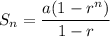
Therefore, sum of the first 5 terms: