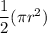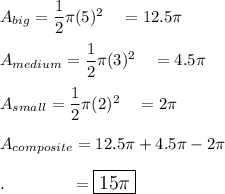Answer: Perimeter = 6π ≈ 18.84
Area = 15π ≈ 47.10
Explanation:
This is a composite of a big semicircle with diameter of 10 --> radius (r) = 5
plus a medium semicircle with diameter of 6 --> r = 3
minus a small semicircle with diameter of 4 --> r = 2
Perimeter of a semicircle =
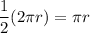
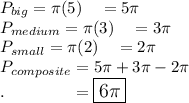
Area of a semicircle =