Question

Find the x-coordinates of the two points on the curve

y=x-1/x at which the tangent is parallel to the straight line 4y= x + 8. (4 marks)​

Answer 1

Answer: x = {-2, 2}

Explanation:

Tangent means it is touching. Find the intersection of the two equations.

Solve the linear equation for y, then set the two equations equal to each other.

`4y=x+8\qquad \rightarrow \qquad y=(x+8)/(4)`

`(x-1)/(x)=(x+8)/(4)\\\\\\\text{Cross multiply and solve for x:}\\4(x-1)=x(x+8)\\4x-4=x^2+8x\\.\qquad 0=x^2+4x+4\\.\qquad 0=(x+2)^2\\.\qquad 0=x+2\\.\qquad x=-2`

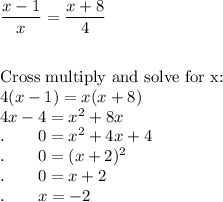
To find the next point that is parallel to the linear equation and tangent to the curve, we need to use the linear equation with slope (m) =
`(1)/(4)` and unknown b.

Let's try b = 0, then the equation of the linear equation is:
`y=(1)/(4)x`

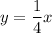
Set the equations equal to each other and solve for x:

`(x-1)/(x)=(x)/(4)\\\\\\4(x-1)=x^2\\4x-4=x^2\\.\qquad 0=x^2-4x+4\\.\qquad 0=(x-2)^2\\.\qquad 0=x-2\\.\qquad x=2`

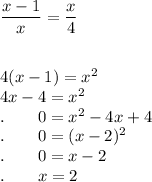
This works!!! If it didn't work, we would have tried other values for b until we arrived at a solution.